基于电势的解析布局
基本概念
布局的定义
布局问题可以描述为一个超图问题,可以定义为如下: $$G = (V,E,R)$$ 其中$V$表示元器件(顶点)集合,$E$表示网表(超边)集合,$R$表示布局区域。在$V$中$V_m$表示可移动器件的集合,$V_f$表示固定块集合。令$n=|V_m|$表示可移动布局对象的个数。 一个合法的布局解决方案应该要满足下面三个要求:
- 在布局区域中使用足够的空闲位置容纳每个器件
- 每个元器件在水平方向上要和布局行的边界对齐
- 元器件和宏组件不能有重合
基于上述的合法性限制,布局的目标就是最小化网表的总$HPWL$,假定$\mathbf{v}=(\mathbf{x},\mathbf{y})$表示一个布局的方案,其中$\mathbf{x}={x_i|i \in V_m}$表示所有元器件的水平坐标,$\mathbf{y}={y_i|i \in V_m}$表示元器件的垂直坐标,则对于每个网表$e(e \in E)$,其半周线长的定义如下:
$$HPWL_e(\mathbf{v}) = \max_{i,j \in e}|x_i-x_j|+\max_{i,j \in e}|y_i-y_j| \tag 1$$ 则总半周线长定义为: $$HPWL(\mathbf{v}) = \sum_{e \in E} HPWL_e(\mathbf{v})$$ 布局问题定义为如下: $$\min_\mathbf{v}HPWL(\mathbf{v}),使得\mathbf{v}是一个合法的布局方案 \tag 2$$
全局布局的定义
把布局区域$R$按$m\times m$划分成一个一个的格子(称作bin),这些格子的集合是B,其中$\rho_b(\mathbf{v})$表示每个b的密度,其定义如下: $$\rho_b(\mathbf{v}) = \sum_{i \in V} l_x(b,i)l_y(b,i) \tag 3$$ 其中$l_x(b,i)$和$l_y(b,i)$分别表示元器件i和格子b之间的水平和垂直重合,全局布局的定义如下: $$\min_\mathbf{v}HPWL(\mathbf{v})\ s.t.\rho_b(\mathbf{v})\leq \rho_t, \forall b \in B \tag 4$$
线长平滑化
每一个网表$e={(x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)}$有n个引脚 ,对数和指数(LSE)在水平轴x方向的线长平滑公式如下:
$$W_e(\mathbf{v}) =\gamma \begin{pmatrix} ln\sum_{i \in e} exp(\frac{x_i}{\gamma})+ln\sum_{i \in e} exp(\frac{-x_i}{\gamma}) \end{pmatrix} \tag{5}$$
其中${\gamma}$是平滑参数,不能随意设置的足够小。
权重平均(WA)在水平轴x方向的线长平滑公式如下:
$$W_e(\mathbf{v}) = \begin{pmatrix} \frac{\sum_{i \in e} x_iexp(\frac{x_i}{\gamma})}{\sum_{i \in e} exp(\frac{x_i}{\gamma})}-\frac{\sum_{i \in e} x_iexp(-\frac{x_i}{\gamma})}{\sum_{i \in e} exp(-\frac{x_i}{\gamma})} \end{pmatrix} \tag{6}$$
密度惩罚
在实际的布局当中,$|B|$个格子的密度都需要满足限制,我们把这些限制用一个惩罚项$N(\mathbf{v})$来表示,当惩罚项$N(\mathbf{v})=0$时所有的密度都满足,其定义如下: $$\rho_b(\mathbf{v})\leq \rho_t, \forall b \in B \iff N(\mathbf{v})=0 \tag 7$$ 用二次惩罚项来表示如下: $$N(\mathbf{v})=\sum_{b \in B }(\widetilde \rho_{b}(\mathbf{v})- \rho_t)^2 \tag 8$$ 其中$\widetilde \rho_{b}$表示在Naylor et al. 2001中定义的铃状的平滑密度函数,密度惩罚$N(\mathbf{v})$也用来表示系统的势能。
非线性布局优化方程
利用惩罚因子$\lambda$目标函数$f(\mathbf{v})$的定义: $$\min_\mathbf{v} f(\mathbf{v}) = W(\mathbf{v})+\lambda N(\mathbf{v}) \tag 9$$ 也可以用拉格郎日乘子法写成下面的形式: $$\min_\mathbf{v} f(\mathbf{v}) = W(\mathbf{v})+\sum_{b \in B}\lambda_b|\widetilde \rho_{b}(\mathbf{v})- \rho_t| \tag{10}$$ 其中$\lambda_b$表示每个格子b的密度限制参数乘子
静电系统建模(eDensity)
电势和电场分布由系统中的所有元素决定,在网表中的每个节点(元器件或者宏块)带正电苛的粒子i。粒子的带电量$q_i$表示为节点的面积$A_i$,根据洛仁力量定律(Lorentz force law)定义的电力$F_i=q_i \xi_i$,会引起可移动的节点i的运动,$\xi_i$表示节点i的布局电场。同样的$N_i=q_i \psi_i$表示节点的势能,$\psi_i$表示器件i的电势大小。根据库仑定律,器件i的电场和电势是系统中剩余器件共同作用的叠加。
整个布局的电苛密度分布表示为$\rho(x,y)$,$\xi_x(x,y)$表示水平电场的分布函数,表示$\psi(x,y)$电势分布函数。
静电平衡系统建模
布局系统和静电系统的建模图:
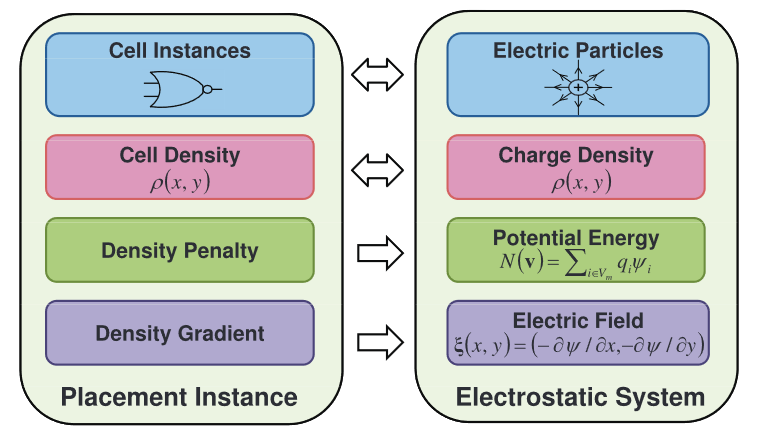
根据建模规则,把均匀分布的全局布局约束同静电平衡的系统状态联系起来,电力会指引电苛(元器件)向着平衡状态的方向移动。根据高斯法则,电场等于电势的负梯度,如下定义: $$\xi(x,y)=(\xi_x,\xi_y)=-\nabla\psi(x,y)= \begin{pmatrix} -\frac{\partial \psi(x,y)}{\partial x},-\frac{\partial \psi(x,y)}{\partial y} \end{pmatrix} \tag{11}$$ 电苛的密度函数等于电场函数的散度 $$\rho(x,y)=\nabla \cdot \xi(x,y)=-\nabla \cdot \nabla\psi(x,y)=- \begin{pmatrix} \frac{\partial ^2\psi(x,y)}{\partial x^2}+\frac{\partial ^2\psi(x,y)}{\partial y^2} \end{pmatrix} \tag{12}$$ 静电系统如果只有正电苛那么只会产生排斥力,相应的静电平衡状态会把所有的器件沿着边界进行分布,因为在边界上可以违反布局约束。因此需要从密度分布当中移除直流组件(即0频率组件)去产生负电苛,从而整个布局区域的密度函数整体变为0。 具体一点说,因为密度函数把所有的对象转化成了正电苛,因此就产生了一个正电苛密度分布。然后就是当直流电移除后,需要填充的区域的电量会比原来有直流电的时候的电量更小,因此就变成了负电苛。同时过于填充的区域依然是正电苛(但是电量比原来小了)。正电苛多的地方会向着负电苛区域移动,相互中和,从而达到一个静电平衡的状态。使得整个系统在布局区域内达到电苛密度为0并且电势也降到0。 这样就把布局的密度惩罚和梯度建模为了势能和电场。‘
密度惩罚和梯度
势能的总和等于新的元器件集合$V^{’}$中所有带电元素的势能之和,这些元素包含了来自$V$中的可移动节点、固定宏节点,也包含了下一步要讨论的填充节点和暗节点。
填充节点插入
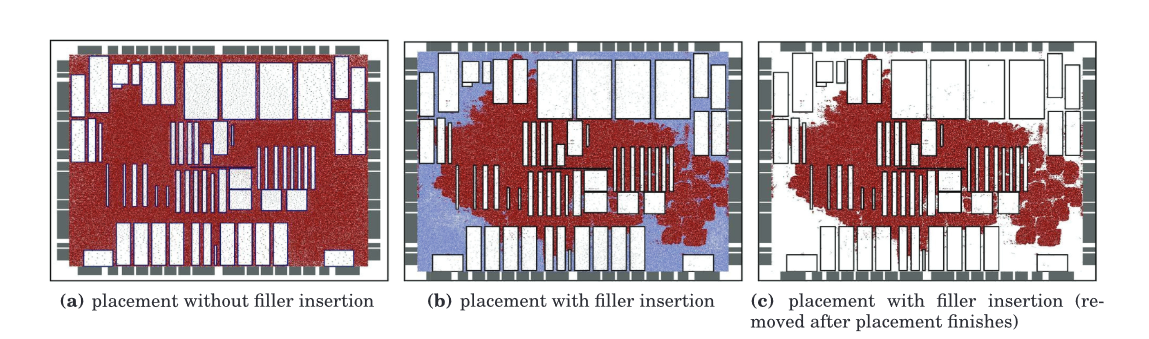
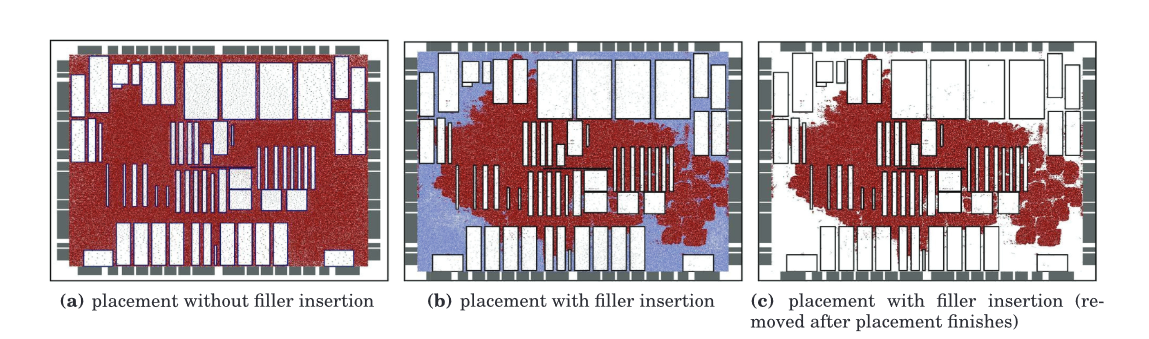
上图中的黑色长方形表示宏元器件,红点表示标准元器件,蓝点表示填充节点,随着填充节点充斥在空白区域,有了更小的总线长,同时器件也挤压在了一起,相互离的更近。
$A_m$表示可移动节点的总面积,$A_{ws}$表示空白空间的总面积。如果目标密度是$\rho_t \geq \frac{A_m}{A_{ws}}$,均匀密度分布会过度的把器件平铺,引起了不必要的线长增加。填充节点(filler cell)都是等尺寸(距形)的,可以移动和并且是断连(0引脚)。$A_{fc}$表示填充节点的总面积,定义如下: $$A_{fc} = \rho_tA_{ws}-A_m \tag{13}$$ 每个填充节点$i$的面积是$A_i$,这个是由可移动器件的面积分布所决定的。每个填充节点的尺寸是可移动器件的中间80%的平均尺寸。填充节点的插入会增加额外的密度力,这会使得元器件和他的连接器件之间的距离更小,同时也会满足密度约束。全局布局结束以后,所有的填充节点都会删除。
暗节点插入
用一个均匀的网格$R(m\times m)$铺在所有的布局区域上,$R$里面不属于任何布局区域的所有空间都会被划分成一个包含很多长方形格子的集合,每一个格子就是一个暗节点, 对于暗节点的处理方式和固定器件的处理方式一致。$V_d$表示所有的暗节点集合,$A_d$表示所有的节点的总面积。当可移动节点到达布局的边界上时,可移动节点会因为受到暗节点的排斥力而停止。
密度缩放
填充节点插入后,目标密度就变成了$\rho_t = \frac{A_m+A_{fc}}{A_{ws}}$。为了去维持全局等效的密度分布,每一个固定节点或者暗节点$i$的面积$A_i$都需要通过$\rho_t$进行缩放,否则密度力会变得比填充物的密度力更大,并把器件排斥开,固定结点周围的空白区域会被置空,也会增加下图所示的线长开销。
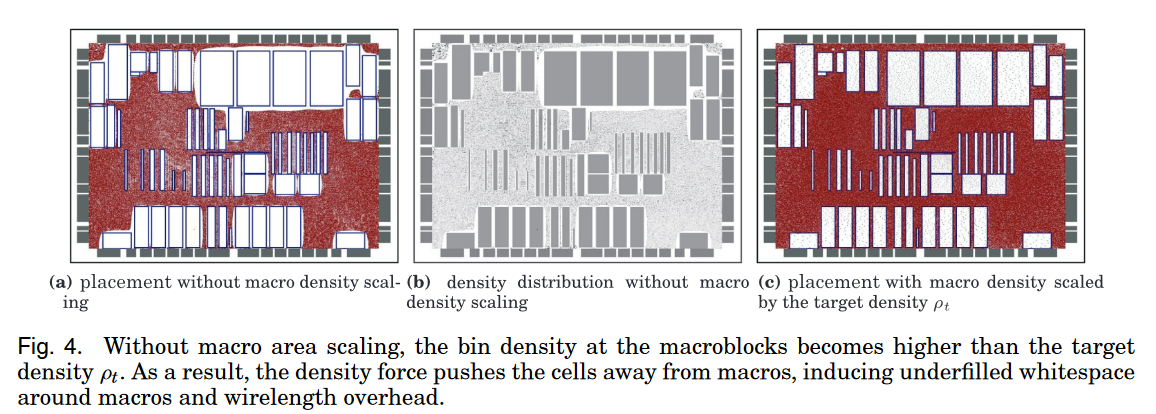 上图中(a)和(b)在没有密度缩放的情况下,在大组件上网格的密度会高于目标密度,从而密度力会把器件从大组件周围推开,从而引起了宏组件周围更多待填充的空白区域和线长开销。
上图中(a)和(b)在没有密度缩放的情况下,在大组件上网格的密度会高于目标密度,从而密度力会把器件从大组件周围推开,从而引起了宏组件周围更多待填充的空白区域和线长开销。
势能计算
$V^{’}=V_m \bigcup V_f \bigcup V_{fc} \bigcup V_d$表示系统中所有元素的集合,对于每一个节点$i \in V^{’}$,$\rho_i$、$\xi_i$和$\psi_i$分别表示该节点的电密度、电场和电势。给定一个可移动器件集合$V_m$和填充节点集合$V_{fc}$的布局方案$\mathbf{v}$,其总的势能如下表示: $$N(\mathbf{v})=\frac{1}{2}\sum_{i \in V^{’} }N_i=\frac{1}{2}\sum_{i \in V^{’} }q_i\psi_i \tag{14}$$ 因为系统的势能会等于所有的电苛的相互作用之和,所以每个单节点需要乘以$\frac{1}{2}$,把重多网格密度约束问题转化成了一个0势能系统的单一势能约束$N(\mathbf{v})=0$。通过引入惩罚因子$\lambda$,一个不受约束的优化问题如下: $$\min_\mathbf{v} f = W(\mathbf{v})+\lambda N(\mathbf{v}) \tag{15}$$ 其中$W(\mathbf{v})$是来自方程6,$f(\mathbf{v})$表示的是最小化的代价函数。因为$W(\mathbf{v})$和$N(\mathbf{v})$都是平滑的,我们可以通过求微分得到如下的梯度向量$\nabla f(\mathbf{v})$: $$\nabla f(\mathbf{v}) = \nabla W(\mathbf{v})+\lambda\nabla N(\mathbf{v})= \begin{pmatrix} \frac{\partial W}{\partial x_1},\frac{\partial W}{\partial y_1},\cdots \end{pmatrix}^T - \lambda(q_1{\xi_1}_x,q_1{\xi_1}_y,\cdots)^T \tag{16}$$
泊松方程和数值计算
根据在3里面定义的eDensity(电密度)公式,使用泊松方程去解决带电势和电场的电苛密度问题。诺伊曼边界条件(the Neumann boundary condition)是用来去合法化全局布局方案。泊松方程是可以数值求解的,其用到了谱方法,有着高精确度并且简单。因此,我们提出该技术在离散网格上局部平滑化电密度。
明确定义的泊松方程
根据高斯准则,电势分布$\psi(x,y)$可以借助泊松方程使用电密度函数$\rho(x,y)$来求解,方程如下所示:
$$\nabla \cdot \nabla\psi(x,y)=-\rho(x,y),(x,y) \in R\tag{17}$$
令$\mathbf{\hat n}$是布局区域的外法向量,$\partial R$是边界。当器件向布局区域的边界上移动时,为了阻止元器件向边界外移动,会停止或者减慢器件的继续向外运动。当器件到达密度函数值域的边界时电密度力会减少到0。因此借助诺伊曼边界条件,边界上就需要定义一个0梯度。 $$\mathbf{\hat n} \cdot \nabla\psi(x,y)=0,(x,y) \in \partial R\tag{18}$$ 此外,在整个布局区域R上电势函数$\psi(x,y)$和密度函数$\rho(x,y)$的积分都需要为0,如下所示 $$\iint_{R} \rho(x,y)=\iint_R\psi(x,y)=0\tag{19}$$ 因此,所有来自电场和电势密度的不定积分所引入的常量因子都是0。方程19也保证了方程17中的偏微分方程有唯一解。克服了定义了在Eisenmann and Johannes [1998]中因定义不清晰的偏微分方程所引起的问题。
基于先前的定义和讨论,整个泊松方程的构建如下: $$\begin{cases} \nabla \cdot \nabla\psi(x,y)=-\rho(x,y) \ \mathbf{\hat n} \cdot \nabla\psi(x,y)=0,(x,y) \in \partial R \ \iint_{R} \rho(x,y)=\iint_R\psi(x,y)=0 \ \end{cases} \tag{20}$$ 不同于以往的基于偏微分方程的布局方法,该论文是基于一个完整的系统模型。密度惩罚是被正式的定义为系统势能。泊松方程是用来去求解电场,它和电量一起共同作用决定了密度梯度,该梯度遵从洛仁力量定律。通过设置电势的积分为0,该偏微分方程的唯一解得到了保证。计算简单且没有额外的线性项。
使用谱方法快速数值求解法
谱方法表示的是把某些偏微分求解看成是基函数(例如是正余弦波)的总和,并且在求和的时候选择系数去满足偏微分方程的边界条件。正弦函数是一个奇函数,同时也是一个周期函数。在每一个周期的边界上,函数值为0,这就很自然的满足了伊曼边界条件。因此我们使用正弦函数作为基函数去表示电场。 因为电密度和电势分别是电场的导数和积分,我们使用余弦函数作为基函数去表示电密度和电势。
基于这样一种在频域中的分解,使用谱方法可以求解泊松方程。通过使用离散余弦变换(DCT, discrete cosine transformation),把原始的密度函数$\rho(x,y)$修改成一个奇且周期的函数形式$\rho _{DCT}(x,y)$。所以新的函数可以分解成一组不同频率上的余弦波振荡,且可以通过DCT来构建。电场函数和电势函数则可以用相似的方法用离散正弦变换(DST)来构建。
对于密度函数具体的修改方式如下:
假定布局区域R被均匀的划分成一个个$m\times m$的的小格子,因此密度口中函数$\rho(x,y)$的定义域为$[0,m-1]\times[0,m-1]$,把密度波映射到负半边则函数的定义域扩展到品了$[-m,m-1]\times[-m,m-1]$,则密度函数变成了偶函数。然后周期是性的把函数的定义域扩展到$[-\infty,+\infty]\times[-\infty,+\infty]$,基于上述的这两个修改,新的密度函数$\rho_{DCT}(x,y)$可以使用DCT来表示。
假定$u$和$v$是0到m-1的整数下标,频率分量分别定义为$w_u=2\pi \frac{u}{m}$和$w_v=2\pi \frac{v}{m}$,同时我们使用$a_{u,v}$表示每个DCT基波函数的系数。由定义可知,所有的$m\times m$系数可以由二维网格上的基波函数乘以密口度函数的积分得到,公式如下所示:
$$a_{u,v}= \frac 1m \sum_{x=0}^{m-1}\sum_{y=0}^{m-1}\rho(x,y)\cos(w_ux)\cos(w_vy) \tag{21}$$ 则所有的先验系数都可以通过快速傅立叶变换一次性求得。使用余弦系数,新的密度函数$\rho_{DCT}(x,y)$可以通过余弦波的和如下表示: $$\rho_{DCT}(x,y)= \sum_{u=0}^{m-1}\sum_{v=0}^{m-1}a_{u,v}\cos(w_ux)\cos(w_vy) \tag{22}$$ 上述方程可以通过调用FFT库快速求解,基于通过方程17和19和在方程22上的余弦表达式,有了如下的势能函数$\psi_{DCT}(x,y)$方程: $$\psi_{DCT}(x,y)= \sum_{u=0}^{m-1}\sum_{v=0}^{m-1} \frac {a_{u,v}}{w_u^2+w_v^2} \cos(w_ux)\cos(w_vy) \tag{23}$$ 根据高斯法则,电场向量是方程11当中势能函数的负梯度,基于方程23定义的势能函数,可以用DCT和DST的形式得到电场的函数表达式$\xi(x,y)=(\xi_{X_{DSCT}},\xi_{Y_{DCST}})$,如下所示: $$\begin{cases} \xi_{X_{DSCT}}= \sum_u\sum_v \frac {a_{u,v}w_u}{w_u^2+w_v^2} \sin(w_ux)\cos(w_vy) \ \xi_{Y_{DCST}}= \sum_u\sum_v \frac {a_{u,v}w_v}{w_u^2+w_v^2} \cos(w_ux)\sin(w_vy) \end{cases} \tag{24}$$ 其中水平分量$\xi_{X_{DSCT}}$是由水平电场的正弦波所构建的,x值在周期结束的时候,也就是在到达布局的边界上的时候,其值为0。垂直分量$\xi_{Y_{DCST}}$同理。这两个分量可以通过FFT库直接求解。 本方法中使用了DCT和DST谱方法去给偏微分方程求解,在这个方法里面密度惩罚建模为系统势能,密度梯度建模为电苛力。
行为和复杂度分析
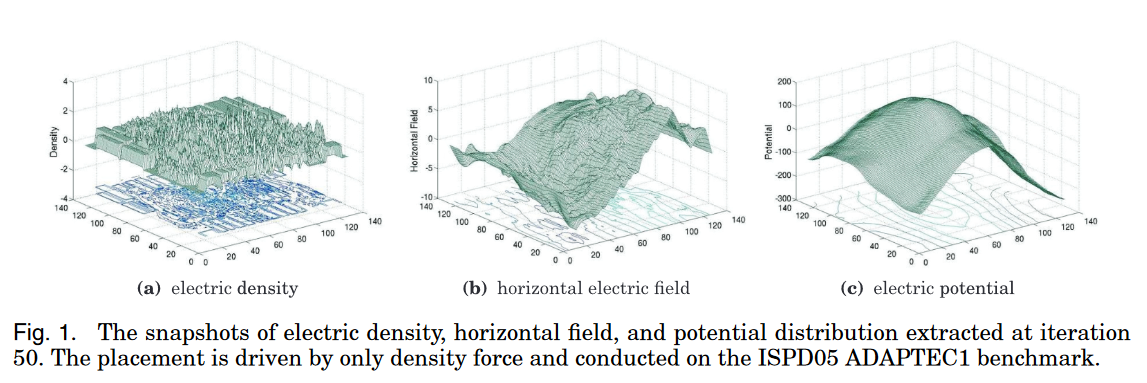
下图表示了一个二维平面的离散密度的电场分布,随着迭代的进行密度的分布也会发生变化,电场的分布也会改变,因此电场会动态的指引器件向欠填充区域流动。从下图当中我们也发现到,在布局区域的边界上,电场变为0。这样的行为就满足了边界条件和全局布局的要求。下图当中的灰点是密度分布,红箭头是电场方向。

假定布局区域上总的有$n^{’}$个器件($n^{’}=|V_m|+|V_{fc}|$)和一个$m\times m$的网格。本方法的总的复杂度主要来自两个方面, 一是密度计算,二是势能和电场的计算。
密度计算。每个迭代中,密度函数是由下面两步完成:
- (1)遍历B中所有的元素去清空器件密度和器件面积到0
- (2)遍历所有的可移动器件和填充器件,对于有重叠的相应网格需要计算每个器件对于相应网格的面积贡献 第一步的时间复杂度是$O(m^2)$,第二步的复杂度是$O(n^{’})$,所以每个迭代产生密度分布的总时间复杂度为$O(m^2+n^{’})$。
势能电场计算。每个迭代会调用四次FFT库去解决方程21、23和24。每个2维的FFT库的复杂度为$O(m^2\log m^2)=O(2m^2\log m)=O(m^2\log m)$,因此总的复杂度为$O(m^2\log m)$
一般来说,我们的数值方法每个布局迭代的时间复杂度为$O(n^{’}+m^2 \log m)$。因为网格的数量规模通常和器件是同一个数级规模(可以确保离散后的准确性),所以有$O(n^{’})=O(m^2)$,并且总的时间复杂度为$O(m^2\log m)$或$O(n^{’}\log n^{’})$。填充器件的加入会增加一些计算时间,但是不会改变整体的计算量级。所有的填充器件和标准器件的平均尺寸一样大,如果效率低的话标准器件会被放大到网格的尺寸,使得填充物的总数量不会超过$O(m^2)$。而且因为填充器件的个数规模和可移动器件的规模是一样的,会有$n=O(n^{’})$,因此总的时间复杂度为$O(n\log n)$,$n$为可移动器件的个数。
离散网格上的局部平滑
电密度的全局平滑可以通过方程11和方程12得到。因为每个单元网格的大小通常会比器件的尺寸要大,所以单元网格内部的局部运动是不能在密度函数上反应出来的,从而使平滑性变差。因此我们提出了一种局部平滑技术使得方程14中的密度函数可以反应出每个单元网格内部的任何细微的运动。如下图表示的是一个一维的例子,其中$w_i$表示的是器件的宽度,$w_b$表示的是单元格的宽度;然后,$c_i$表示的是器件中心的坐标,$c_b$单元格中心的坐标。
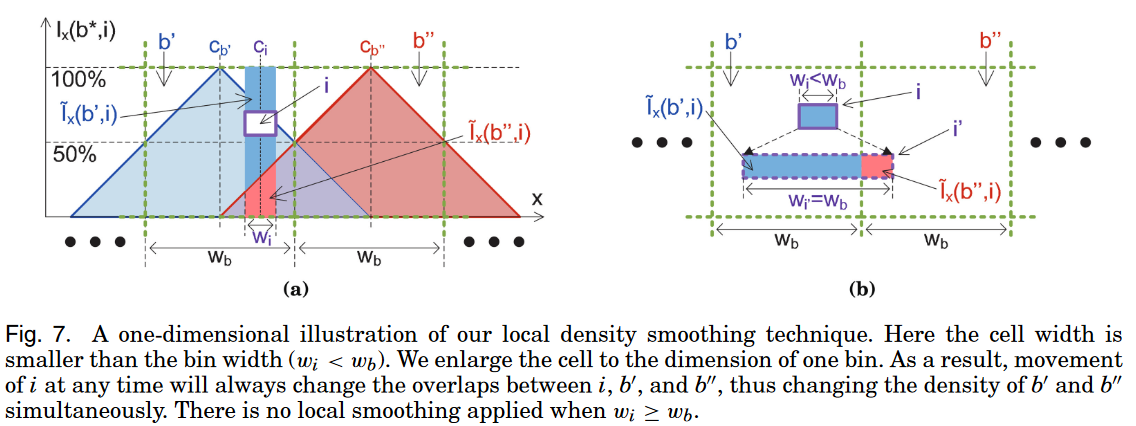 $l_x(i,b)$表示的是原始的器件和单元格在水平方向上的重叠,$\hat l_x(i,b)$表示的是平滑后的水平方向上的重叠。则有如下:
$$\hat l_x(i,b)=\begin{cases}
(1.0-\frac {c_i-c_b}{w_b})\times w_i:c_i \in [c_b-w_b,c_b+w_b]\
0:c_i \in [-\infty,c_b-w_b]\cup[c_b+w_b,+\infty]
\end{cases} \tag{25}$$
随着器件向右移动,器件对单元格$b’$的密度贡献线性减少,对单元格$b’’$贡献线性增加。当器件在两个单元格坐标$c_{b’}$和$c_{b’’}$的中间的时候,也就是$c_i$在$[c_{b’},c_{b’’}]$上的时候,器件$i$对于两个单元格的总贡献是不变的,且贡献为$w_i$。这种平滑的效果是等价于器件的拉伸和器件密度降低的组合,保持了目标代价函数的可解析。对于每一个器件$i$,局部平滑化进行如下操作:
$l_x(i,b)$表示的是原始的器件和单元格在水平方向上的重叠,$\hat l_x(i,b)$表示的是平滑后的水平方向上的重叠。则有如下:
$$\hat l_x(i,b)=\begin{cases}
(1.0-\frac {c_i-c_b}{w_b})\times w_i:c_i \in [c_b-w_b,c_b+w_b]\
0:c_i \in [-\infty,c_b-w_b]\cup[c_b+w_b,+\infty]
\end{cases} \tag{25}$$
随着器件向右移动,器件对单元格$b’$的密度贡献线性减少,对单元格$b’’$贡献线性增加。当器件在两个单元格坐标$c_{b’}$和$c_{b’’}$的中间的时候,也就是$c_i$在$[c_{b’},c_{b’’}]$上的时候,器件$i$对于两个单元格的总贡献是不变的,且贡献为$w_i$。这种平滑的效果是等价于器件的拉伸和器件密度降低的组合,保持了目标代价函数的可解析。对于每一个器件$i$,局部平滑化进行如下操作:
- 如果$w_i< w_b$,把器件的宽度从$w_i$拉长到$w_b$,并且把器件密度从1.0减少到$w_i/w_b$
- 如果$w_i\ge w_b$,保持原来的细胞宽度和密度 这种平滑技术在不同的粒度和器件尺寸上都是一样的,在每个迭代更新密度图的时候都会用到这种平滑技术。因为对于每个器件来说只有有限个邻近的单元格会被该器件影响到,所以其时间复杂度是恒定不变的,因此计算复杂度并未发生变化。
非线性优化
布局问题是NP完全问题。如方程9中所示,目标函数由一个凸线长函数和一个非凸密度函数组成,非凸函数加大了现代凸规划方法求解的难度。本部分先介绍先前非线性布局当中使用到的共轭梯度方法,讨论线搜索的效率瓶颈。这篇论文是首次在全局布局优化中使用Nesterov’s方法和Lipschitz常数预测。
共轭梯度法
下图为第k个迭代的时候的算法,其中第4行是线搜索算法,存在较多的问题。

使用Lipschitz常数预测的Nesterov’s方法
和CG法类似,但是Nesterov法只需要一阶导数和线性的内存开销。Nesterov法旨在解决Hilbert空间$H$里的凸规划问题。和大多数和凸规划方法不同,Nesterov法构建了一个不松弛的最小化的点序列${\mathbf{u}_k}_0^\infty$。算法2如下所示,表示了第k次迭代的处理算法,这次迭代主要聚焦在$\min{f(\mathbf{u})|\mathbf{u} \in H}$这个问题上,该问题有非空的最小值集合$U^*$。算法2如下所示:

上述算法中,$\mathbf{u}$是凸规划问题的解,$\mathbf{v}$是用来计算步长的参考解,$a$是优化参数,$\alpha$是步长。迭代开始时($k=0$),该方法会初始化$\mathbf{v}_0 \in H,a_0=1,\alpha_0=\frac{||\nabla f(\mathbf{v}_0)-\nabla f(\mathbf{z})||}{||\mathbf{v}_0-\mathbf{z}||}$。其中$\mathbf{z}$是$H$中的任意一个点且$\mathbf{z}\neq\mathbf{v}_0$。Nesterov法的收敛率是$O(1/k^2)$,上述算法的第2行主要就是加速收敛,如果要达到预期的收敛率,则步长$\alpha_k$在每一个迭代中都要满足下列方程:
$$f(\mathbf v_k)-f(\mathbf v_k-\alpha_k\nabla f(\mathbf v_k))\geq0.5\alpha_k||\nabla f(\mathbf v_k)||^2 \tag{26}$$
Nesterov法的上界错误率方程27所示。
定理 5.1。假定$f(\mathbf u)$是一个在$C^{1,1}(H)$和$U^* \neq \varnothing$上的凸函数,其中$C^{1,1}(H)$表示梯度函数$\nabla f(\mathbf u)$是Lipschitz连续的。现有$\mathbf u\in U^*$,并且$L$是梯度函数$\nabla f(\mathbf u)$的Lipschitz常数。则由上述算法2输出的$\mathbf{u}_k$会存在以下公式:
$$f(\mathbf u_k)-f(\mathbf u^*) \geq \frac{4L||\mathbf v_0-\mathbf u^*||^2}{(k+2)^2} \tag{27}$$
定义 5.2。给定一个函数$f \in C^{1,1}(H)$,并且$L$是梯度函数$\nabla f(\mathbf u)$的Lipschitz常数,则对于任意的$\mathbf u,\mathbf v \in H$有 $$||\nabla f(\mathbf u)-\nabla f(\mathbf v)||\leq L||\mathbf v-\mathbf u||, \tag{28}$$
并且$\nabla f(\mathbf u)$是Lipschitz连续的。因为Nesterov法使用了二分查找法去计算最大步长所以,在每一个迭代中目标函数都需要评估$O(\log L)$次,则时间复杂度增加到了$O(n\log n\log L)$。相反,我们使用步长预测去加速我们的布局算法。正如在论文Nesterov [1983]中讨论的,如果梯度函数的Lipschitz常数已知,我们可以设置步长为Lipschitz常数的倒数去满足方程26,不会引起任何开销。但是预测准确全局布局梯度函数的Lipschitz常数往往会比较困难,因为有如下原因:
- 因为密度函数的加入,使得目标函数非凸,因此定理5.1不满足。
- 因为要动态的调整平滑系数(方程6),线长函数会随着迭代而改变。
- 因为要在运行的时候做力平衡,所以在密度函数上方程15中的惩罚因子$\lambda$会随着迭代而变化。
因为上述特性,全局布局函数是非凸且动态变化的,所以需要一个随着迭代去动态估计Lipschitz常数为$\widetilde L$。基于方程28,分别设定函数$\mathbf x$和$\mathbf y$的值为当前参考值$\mathbf y_k$和上一次迭代的参考值$\mathbf y_{k-1}$,则$\nabla f(\mathbf y_k)$Lipschitz常数可以用如下公式逼近:
$$\widetilde L_k = \frac {||\nabla f(\mathbf y_k)-\nabla f(\mathbf y_{k-1})||} {||\mathbf y_k-\mathbf y_{k-1}||} \tag{29}$$
则根据上述讨论可以知道步长为:
$$\alpha_k=\frac{1}{\widetilde L_k}$$
上述的方法是高效的,因为:
- (1)都是已知的,没有额外的计算。
- (2)相比较于随机的选择$\mathbf x$和$\mathbf y$,前后迭代的$\mathbf y_k$和$\mathbf y_{k-1}$的值比较接近,则$||\mathbf y_k-\mathbf y_{k-1}||$值相对较小,可以防止对Lipschitz常数的估计精度过低,并且防止过度估计步长$\alpha_k$。
在实验当中也证实了,这种估计法有效的加速了计算过程。
预处理
预处理减少了问题的条件数,使得原本的问题更加适合数值求解法求解。传统的预处理方法是计算并且反转目标函数$f$的海森矩阵$H_f$。因为密度函数是非凸的所以在非线性布局上还没人使用预处理。预处理梯度向量$\nabla f_{pre}=H^{-1}\nabla f$可以平滑化数值优化,加速函数的收敛。
因为全局布局的目标函数是高度非线性并随迭代变化,再者问题的规模往往是百万级别,这就使得每次迭代的时候计算海深矩阵的代价就太高了,且不实际。为了可以在实际中计算海森矩阵,我们使用只使用海森矩阵对角项的雅格比预处理来近似求解,如下所示:
$$\mathbf H_{\mathbf f_{\mathbf x,\mathbf x}}= \begin{Bmatrix} \frac {\partial^2 f} {\partial x^2_1} & \frac {\partial^2 f} {\partial x_1\partial x_2} &\cdots &\frac {\partial^2 f} {\partial x_1\partial x_n} \\ \frac {\partial^2 f} {\partial x_2\partial x_1} & \frac {\partial^2 f} {\partial x^2_2} &\cdots &\frac {\partial^2 f} {\partial x_2\partial x_n} \\ \vdots & \vdots &\ddots &\vdots\\ \frac {\partial^2 f} {\partial x_n\partial x_1} & \frac {\partial^2 f} {\partial x_n\partial x_2} &\cdots &\frac {\partial^2 f} {\partial x^2_n} \\ \end{Bmatrix} \approx\begin{Bmatrix} \frac {\partial^2 f} {\partial x^2_1} & 0 &\cdots &0 \\ 0 & \frac {\partial^2 f} {\partial x^2_2} &\cdots &0 \\ \vdots & \vdots &\ddots &\vdots \\ 0 & 0 &\cdots &\frac {\partial^2 f} {\partial x^2_n} \\ \end{Bmatrix}=\widetilde H_{\mathbf f_{\mathbf x,\mathbf x}}\tag{30}$$
根据上述近似,同理可以计算$\mathbf H_{\mathbf f_{\mathbf y,\mathbf y}}$,因此可以计算出$\mathbf H_{\mathbf f}$。通过方程15则有$\frac {\partial^2 f(\mathbf v)} {\partial x^2_i}=\frac {\partial^2 W(\mathbf v)} {\partial x^2_i}+\lambda\frac {\partial^2 N(\mathbf v)} {\partial x^2_i}$,我们可以精准的估计出$\frac {\partial^2 W(\mathbf v)} {\partial x^2_i}和\frac {\partial^2 N(\mathbf v)} {\partial x^2_i}$的值,保证预处理的可行性。方程6中对线长函数微分的代价会比较高,所以我们使用器件$i$的顶点度来计算,如下:
$$\frac {\partial^2 W(\mathbf v)} {\partial x^2_i}=\sum_{e\in E_i}\frac {\partial^2 W_e(\mathbf v)} {\partial x^2_i}\implies |E_i|,\tag{31}$$
其中$E_i$表示和器件i相关的网表子集。方程14中所表示的密度函数是非凸的,就使得传统的预处理方法不能够得到预期的性能。方程32使用了二阶微分:
$$\frac {\partial^2 N(\mathbf v)} {\partial x^2_i}=q_i\frac {\partial^2 \psi(\mathbf v)} {\partial x^2_i}=q_i\frac {-\partial \xi_{i_x}(\mathbf v)} {\partial x_i}= q_i。\tag{32}$$
所以使用线性项$q_i$作为密度预处理,使用上述的近似来表示$\widetilde H_{\mathbf f_{\mathbf x,\mathbf x}}$会有如下方程:
$$\widetilde H_{\mathbf f_{\mathbf x,\mathbf x}}=\begin{Bmatrix} |E_1|+\lambda q_1 & 0 &\cdots &0 \\ 0 & |E_2|+\lambda q_2 &\cdots &0 \\ \vdots & \vdots &\ddots &\vdots \\ 0 & 0 &\cdots &|E_n|+\lambda q_n \\ \end{Bmatrix} \tag{33}$$
因此可以计算出预处理的梯度为$\nabla f_{pre}=\widetilde {\mathbf H}_{\mathbf f}^{-1}\nabla f$
全局布局算法
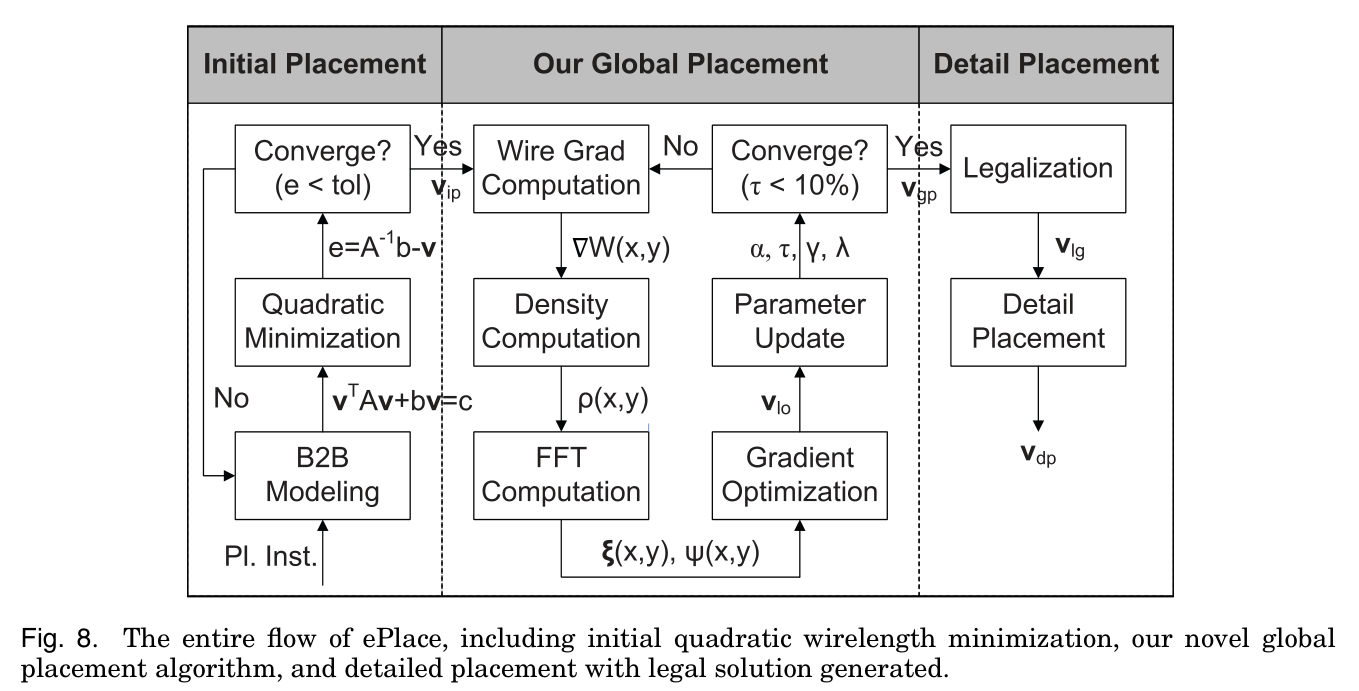
如下图8所示表示的是,ePlace的整个布局流程:
 其中分为三个阶段:
其中分为三个阶段:
- (1)初始布局 :使用B2B网络模型最小化二次项线长函数,得到初始布局的输出结果$\mathbf v_{ip}$。
- (2)全局布局:根据电势理论优化器件的位置
- (3)细节布局:全局布局完成后,移除所有的填充器件,并使用FastDP进行合法化和离散优化。
从上面的讨论中我们知道,CG法和Nesterov法都是用来解决方程15中不受限的优化问题,为了去改善优化结果和收敛率,我们使用了一种自适应参数调整法。
自适应参数调整法
网格的尺寸
在整个全局布局阶段,网格的大小都是固定的。这是在粒度和效率之间的平衡。越大的尺寸往往代表的是高效低准确率,越小的尺寸则相反。比较大的尺寸也会带来一些额外的问题,更多的器件会有相同的密度力。这些器件糅合在一起,有相同的运动轨迹,也就是说这些器件会在相邻区域间发生密度震荡,阻止器件的扩散。
这篇论文中风格的尺寸大小是基于器件和填充器件的个数来计算,把网格的尺寸设定为$m=\min(\lceil \log_2\sqrt{n{’}} \rceil, 1024)$,设定最大为1024的原因是出于效率考虑。
步长
在Nesterov法中根据方程29可以估计出步长为Lipschitz常数估计的倒数,即$\alpha_k=\frac{1}{\widetilde L_k}$。在CG法中,步长由线搜索来决定的,在搜索间隔中,沿着共轭梯度的方向线搜索会找到局部最优,搜索的间隔$\alpha_k^{\max}$是动态的调整的。初始的间隔$\alpha_0^{\max}$和单元格的大小成线性关系$\alpha_0^{\max}=kw_b$,其中$w_b$是单元格宽度。实际设置$k=0.044$可以得到较好的布局质量,并且$\alpha_k^{\max}$需要基于当前最优步长$\alpha_{k-1}$进行更新,如下所示:
$$\alpha_k^{\max}=\max(\alpha_0^{\max},2\alpha_{k-1}),\alpha_k^{\min}=0.01\alpha_k^{\max} \tag{34}$$ 通过方程34,如算法1的第4行所示,GSS可以计算出第k次迭代的步长$\alpha_k$。线搜索会在间隔缩小到$\alpha_k^{\min}$时停止,所以得到的步长$\alpha_k$不一定是局部最优。
惩罚因子
为了去平衡密度和线长的力,在方程35中设定惩罚因子的初始值为:
$$\lambda_0=\frac {\sum_{i \in V_m^{’}}\mid W_{x_i} \mid+\mid W_{y_i} \mid} {\sum_{i \in V_m^{’}}q_i(\mid \xi_{x_i} \mid+\mid \xi_{y_i} \mid)} \tag{35}$$ 其中$W_{x_i}=\frac{\partial W}{\partial x_i},W_{y_i}=\frac{\partial W}{\partial y_i}$,$\xi_{x_i}$是节点i的水平电场,$\xi_{y_i}$是节点i的垂直电场。
因为线长和密度都是随着迭代变化的,为了去适应这种实时的变化,惩罚因子也需要时间更新,我们通过如下的式子去更新因子:
$$\lambda_k=u_k\lambda_{k-1}$$
令$\Delta HPWL_k=HPWL(\mathbf v_k)-HPWL(\mathbf v_{k-1})$,则$u_k$的定义如下:
$$u_k=u_{0}^{-\frac{\Delta HPWL_k}{\Delta HPWL_{ref}}+1.0}(u_0=1.1,\Delta HPWL_{ref}=3.5\times10^5) \tag{36}$$
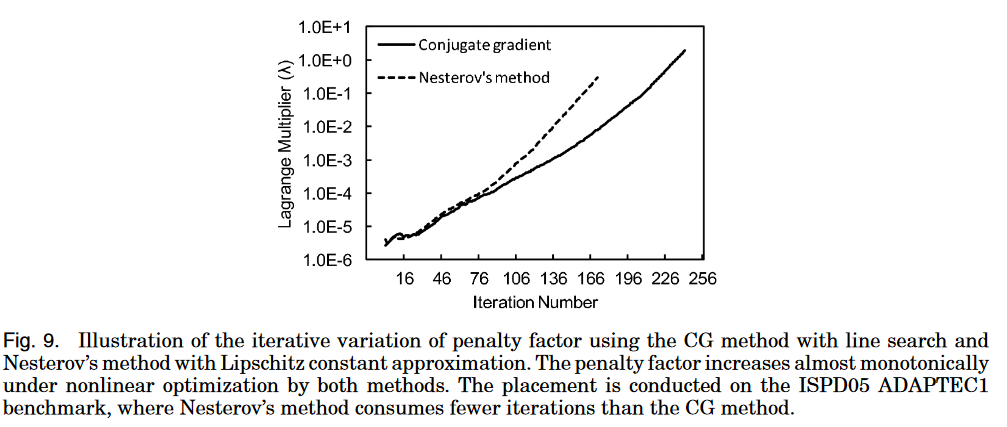
如下图所示,不管是在CG法和Nesterov法上,随着迭代的进行因子的值在增加。
密度溢出
全局布局当重叠足够小的时候会结束,接下来就是要处理合法化和细节布局了。使用如下的密度溢出值$\tau$,公式如下:
$$\tau=\frac {\sum_{b \in B}\max(\rho_b^{’}-\rho_t,0) A_{b}} {\sum_{i \in V_m}A_i} \tag{37}$$
其中,$A_{b}$是单元格面积,$A_{i}$是可移动器件面积。$\rho_b^{’}$是只和可移动器件相关的单元格$b$的密度。当密度溢出的值$\tau\leq\tau_{min}$时,全局布局停止。
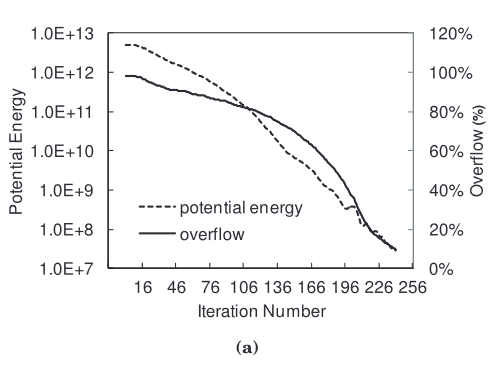
线长系数
实验中显示,收敛结果和布局结果对于平滑参数$\gamma$的变化比较敏感。为了在全局上让更多的的器件逃离高密度区域,本论文中的方法在迭代早期放松平滑参数。在后期阶段,当局部调整占主导的时候,参数值变小使得平滑的线长接近HPWL。
同时较小尺寸的单元格密度对于器件的运动会更加敏感,相反越的尺寸就越不敏感。因此设置平滑参数$\gamma$为密度溢出和单元格宽度的函数。通过减少平滑参数的值,为了去减少剩余的重叠,只需要允许可以局部移动的HPWL不敏感的器件运动。我们所提到的这些HPWL不敏感的器件,指的是它们的运动不会改变器件相关网表的HPWL值,也可以理解成这些器件离网表的边界相对而言比较远。对于 迭代的后期,为了使得线长平滑的收敛,只允许在布局平面上有较小的扰动。所以,因为我们的目的是增加线长建模的准确性,对应的线长力会变得更强去只允许有小规模的运动,也就是较小的平面扰动。如下图所示,最终平滑的HPWL收敛到了HPWL:
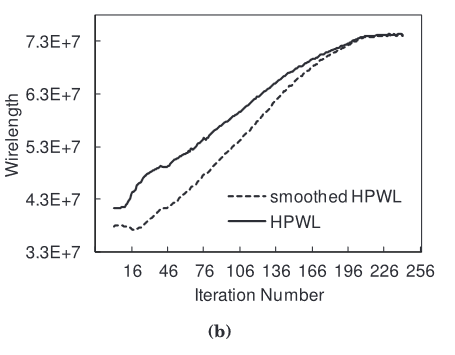
在本论文的实验中显示,如下公式建模平滑系数会有比较好的布局结果,公式如下:
$$\gamma(\tau)=8.0w_b\times10^{k\tau+b} \tag{38}$$
密度溢出通过在开始为100%,结束的时候为10%(终止条件),根据经验调整有$\gamma(\tau=1.0)=80w_b$,有$\gamma(\tau=0.1)=0.8w_b$,则可以计算出$k=\frac{20}{9},b=-\frac{11}{9}$。
全局布局
下图为ePlace全局布局算法的整体流程:

对算法的详细解释如下:
- 输入参数:
- $\mathbf v_0=\mathbf v_{ip}$表示的是初始布局中的输出结果,标准器件是放置在区域中间,填充器件是随机的分布在整个布局区域$R$上。
- $m\times m$网格拆分规模
- 最小的密度溢出$\tau^{\min}$
- 最大的迭代次数为3000
- 第1行把布局区域R拆分成$m\times m$的网格
- 第2行初始化密度惩罚因子
- 第3行初始化最大间隔(这个在调用CG算法的时候会用到,如果是Nesterov法的话不会用到)
- 第5行定义了目标函数$f_k$
- 第6行计算线长梯度和密度分布
- 第7行使用FFT库去计算场和势能
- 第8行计算密度梯度
- 第9行计算目标函数的总梯度
- 第10行调用非线性方法(Nesterov法或者CG法)求解新的布局结果
- 第11行更新非线性方法需要的参数
- 第12行去判定是不是满足终止条件
- 最后返回全局布局的结果。
随着迭代的运行,标准器件会从过填充的区域分散到待填充的区域,密度力会把无连接的填充器件推向布局的边界。最后所有的标准器件会收敛到一个稳定状态,此时系统和势能和线长处于可以接受的状态。