警告
本文最后更新于 2022-12-11,文中内容可能已过时。
2021秋作业1-分治
1. 找出整数数组中第K大的数
215.Kth Largest Element in an Array (Medium)
Given an integer array nums and an integer k, please return the k-th largest element in the array.
Your algorithm’s runtime complexity must be in the order of O(n), prove the correctnes-sand analyze the complexity.(k is much smaller than n, n is the length of the array.)
Example 1:
1
2
| Input: nums = [3,2,1,5,6,4], k = 2
Output: 5
|
Example 2:
1
2
| Input: nums = [3,2,3,1,2,4,5,5,6], k = 4
Output: 4
|
Constraints:
Solution:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int idx = 0;
vector<int> numL;
vector<int> numR;
for (int i = idx + 1; i < nums.size(); i++) {
if (nums[i] > nums[idx]) {
numR.push_back(nums[i]);
} else {
numL.push_back(nums[i]);
}
}
if (numR.size() == k - 1) {
return nums[idx];
} else if (numR.size() > k - 1) {
return findKthLargest(numR, k);
} else {
return findKthLargest(numL, k - numR.size() - 1);
}
}
};
|
(Page55)Complexity:
如果子实例处在$[n(\frac 34) ^{j + 1} + 1, n(\frac 34) ^{j}]$则说明 算法运行在第$j$期,$X$表示算法整体的元素比较次数,$X_j$表示运行过程处于第j期时的比较次数,则有:
$$X = X_0 + X_1 + X_2 + \dots$$
选择中间区域的概率为$\frac 12$,选择一个中间区域的元素作为中心元后,实例规模减少$\frac 1 4$,因为每一期递归调用期望是两次,则在第$j$期的时候算法期望比较次数为$2n(\frac{3}{4})^j$,则整体的期望比较次数为:
$$E(X)=E[X_0 +X_1+X_2+\dots] \leq \sum_j 2cn (\frac 34)^j \leq 8cn$$
则时间复杂度为$O(n)$。
2. 二叉树邻域最小值
Consider an $n$-node complete binary tree $T$, where $n = 2^d − 1$ for some $d$. Each node $v$ of $T$ is labeled with a real number $x_v$. You may assume that the real numbers labeling the nodes are all distinct. A node $v$ of $T$ is a local minimum if the label $x_v$ is less than the label $x_w$ for all nodes $w$ that are joined to v by an edge.
You are given such a complete binary tree T, but the labeling is only specified in the following:
implicit way: for each node v, you can determine the value xv by probing the node v.
Show how to find a local minimum of T using only O(logn) probes to the nodes of T.

解法:

3. 数组子数组最大和
1800.Maximum Ascending Subarray Sum (Easy)
Given an integer array, one or more consecutive integers in the array form a sub-array. Find the maximum value of the sum of all subarrays.
Please give an algorithm with O(nlogn) complexity
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public:
int findLargestSubArraySum(vector<int>& nums, int start, int end) {
if (start == end) {
return nums[start];
} else if (start > end) {
return -1;
}
int mid = (start + end) / 2;
int subStart = mid;
int subSum = nums[mid];
while (subStart > start && nums[subStart] - 1 == nums[subStart - 1]) {
subStart--;
subSum += nums[subStart];
}
int subEnd = mid;
while (subEnd < end && nums[subEnd] + 1 == nums[subEnd + 1]) {
subEnd++;
subSum += nums[subEnd];
}
int subLSum = findLargestSubArraySum(nums, start, subStart - 1);
int subRSum = findLargestSubArraySum(nums, subEnd + 1, end);
return max(max(subSum, subLSum), subRSum);
}
};
|
4. 查找有序数组指定元素的区间
34.find-first-and-last-position-of-element-in-sorted-array (Medium)
Given an array of integers nums sorted in non-decreasing order, find the starting and ending position of a given target value.
If target is not found in the array, return [-1, -1].
You must write an algorithm with O(log n) runtime complexity.
Example 1:
1
2
| Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]
|
Example 2:
1
2
| Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]
|
Example 3:
1
2
| Input: nums = [], target = 0
Output: [-1,-1]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int l = findFisrt(nums, target);
int h = findFisrt(nums, target + 1);
if (l == nums.size() || nums[l] != target) {
return vector<int> {-1, -1};
}
return vector<int> {l, h - 1};
}
int findFisrt(vector<int>& nums, int target) {
int l = 0;
int h = nums.size();
while (l < h) {
int mid = (l + h) / 2;
if (nums[mid] >= target) {
h = mid;
} else {
l = mid + 1;
}
}
return l;
}
};
|
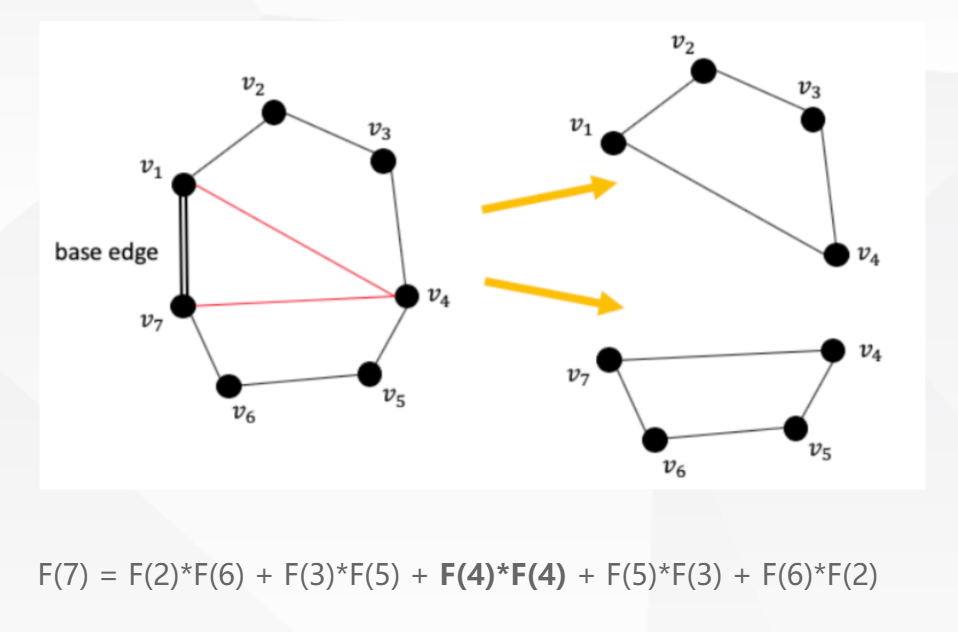
5. 求N多边形可以被切割成多少个三角形
Given a convex polygon with n vertices, we can divide it into several separated pieces, such that every piece is a triangle. When n = 4, there are two different ways to divide the polygon; When n = 5, there are five different ways.
Give an algorithm that decides how many ways we can divide a convex polygon with n vertices into triangles.

6. 归并K个长度为N的有序链表
Given an array of k linked-lists lists, each linked-list is sorted in ascending order. Given an O(knlogk) algorithm to merge all the linked-lists into one sorted linked-list. (Note that the length of a linked-lists is n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
return helpMergeKLists(lists, 0, lists.size() - 1);
}
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode* head = new ListNode(-1);
ListNode* p = head;
while (l1 != NULL || l2 != NULL) {
if (l1 == NULL && l2 != NULL) {
p->next = l2;
l2 = l2->next;
}
if (l1 != NULL && l2 == NULL) {
p->next = l1;
l1 = l1->next;
}
if (l1 != NULL && l2 != NULL) {
p->next = l1->val > l2->val ? l2 : l1;
l1->val > l2->val ? l2 = l2->next : l1 = l1->next;
}
p = p->next;
}
return head->next;
}
ListNode* helpMergeKLists(vector<ListNode*>& lists, const int& start, const int& end) {
if (start > end) {
return NULL;
} else if (start == end) {
return lists[start];
}
int mid = (start + end) / 2;
ListNode* l1 = helpMergeKLists(lists, start, mid);
ListNode* l2 = helpMergeKLists(lists, mid + 1, end);
return mergeTwoLists(l1, l2);
}
};
|
7.Fast Mod Exponentiation
Description
Bob has encountered a difficult problem, and hope you design
an algorithm to calculate pow(a,b) mod 1337, where a is a positive
integer, b is a very large positive integer and will be given in the
form of an array. For example, pow(2,3) mod 1337 is 8.
1 \le a \le 2^{31} - 1,1≤a≤231−1,
1 \le b.length \le 2000,1≤b.lengt**h≤2000,
0 \le b[i] \le 90≤b[i]≤9
bb doesn’t contain leading zeros.
Please give an algorithm with O(\log n)O(logn) complexity.
Input
Line 1: integers
Line 2: an array
Output
One integer
Sample Input 1
Sample Output 1
Sample Input 2
Sample Output 2
Sample Input 3
Sample Output 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #include <stdio.h>
#define MOD_VALUE 1337
int size = 0;
int start = 0;
int count = 0;
int array[2000];
void arrayHalfDivide()
{
array[size - 1] = array[size - 1] / 2;
int i = size - 2;
while (i >= start) {
int curr = array[i] * 5;
array[i] = curr / 10;
array[i + 1] += curr % 10;
--i;
}
if (array[start] == 0 && count > 1) {
count--;
start++;
}
}
int clacFastModExponentation(int base)
{
if (count == 1 && array[size - 1] == 0) {
return 1;
}
if (count == 1 && array[size - 1] == 1) {
return base % MOD_VALUE;
}
int sumMod = 1;
if (array[size - 1] % 2 != 0) {
array[size - 1] = array[size - 1] - 1;
sumMod *= (base % MOD_VALUE);
}
arrayHalfDivide();
int currMod = clacFastModExponentation(base) % MOD_VALUE;
sumMod *= (currMod * currMod) % MOD_VALUE;
return sumMod % MOD_VALUE;
}
int main()
{
int base;
scanf("%d", &base);
char ch;
while ((ch = getchar()) && ch != ']') {
if (ch >= '0' && ch <= '9') {
array[size++] = ch - '0';
count++;
}
}
printf("%d\n", clacFastModExponentation(base));
return 0;
}
|



